刷题笔记之动态规划(三)

打家劫舍

LeetCode 198. 打家劫舍

确定dp数组以及下标的含义
dp[i]: 考虑下标i（包括i）以内的房屋，最多可以偷窃的金额为dp[i]
确定递推公式
分为两种情况：
不偷i房间：dp[i] = dp[i - 1]，即保持上一次的状态。
偷i房间： dp[i] = dp[i - 2] + nums[i]。
那不偷i房间就一定会偷i - 1房间吗？
这里我们对dp数组的定义就很关键，考虑下标i（包括i）以内的房屋,并不是一定会偷i房间，到底偷不偷由递推公式推导得出。
所以状态转移方程为：
dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i]);

dp数组初始化
因为递推公式中有dp[i - 1]和dp[i - 2]，所以应当初始化dp[0]和dp[1]。

1 2	dp[0] = nums[0];//考虑0号房间，最多可以偷窃的金额为nums[0] dp[1] = Math.max(nums[0], nums[1]);//考虑1号（包括1号）以内的房屋，最多可以偷窃的金额选最大

确定遍历顺序
由递推公式可知，dp[i]由dp[i - 1]和dp[i - 2]推导而来，应该从前往后遍历。
1
2
3
for(int i = 2; i <nums.length; i++){
dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i]);
}
打印dp数组
输入：[2,7,9,3,1],结果为：
2 7 11 11 12

完整代码

class Solution {
    public int rob(int[] nums) {
        if (nums.length < 2) {
            return nums[0];
        }
        int[] dp = new int[nums.length];
        dp[0] = nums[0];
        dp[1] = Math.max(nums[0], nums[1]);
        for (int i = 2; i < nums.length; i++) {
            dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i]);
            System.out.println(dp[i]);
        }
        return dp[nums.length - 1];
    }
}

LeetCode 213. 打家劫舍 II

LeetCode题目链接
本题与198. 打家劫舍唯一不同的点是数组首尾相接，形成一个环，这意味着我们要在首尾之间进行取舍。
我们只需要分情况讨论即可。

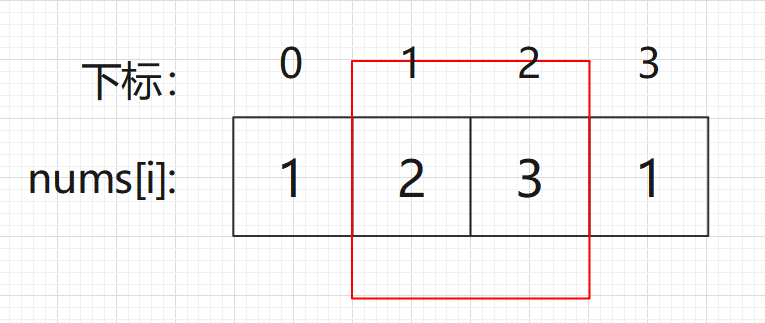
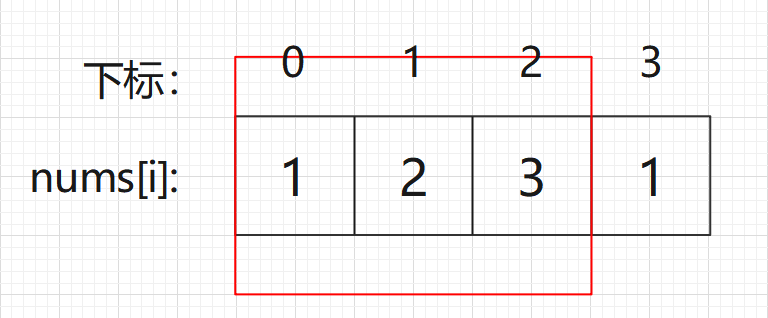
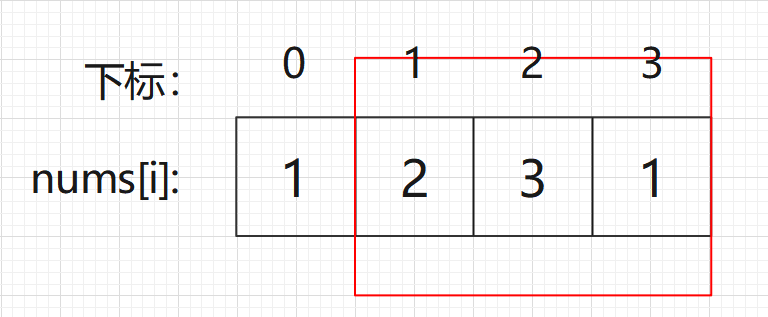
情况一：考虑首尾都不偷
情况二：考虑包含首元素，不包含尾元素

情况三：考虑包含尾元素，不包含首元素
分类情况

这里的关键点是考虑，并不是我把首/尾元素考虑进去，我就一定会偷！并且情况二和情况三都包含情况一，所以只实现情况二和情况三即可。

class Solution {
    public int rob(int[] nums) {
        if (nums.length == 0) {
            return 0;
        }
        if (nums.length == 1) {
            return nums[0];
        }
        return Math.max(myRob(nums, 0, nums.length - 1), myRob(nums, 1, nums.length));
    }
    
    private int myRob(int[] nums, int start, int end) {//解耦
        int x = 0, y = 0, z = 0;
        for (int i = start; i < end; i++) {
            y = z;
            z = Math.max(y, x + nums[i]);
            x = y;
        }
        return z;
    }
}

LeetCode 337. 打家劫舍 III

LeetCode题目链接
本题与前面的dp题目都不同的点是这是一道树形dp，但本质上都是在考虑当前结点可不可取。
首先我们需要明确dp数组的定义：
dp[2]：记录当前结点偷与不偷两个状态得到的金钱，dp[0]代表不偷，dp[1]代表偷

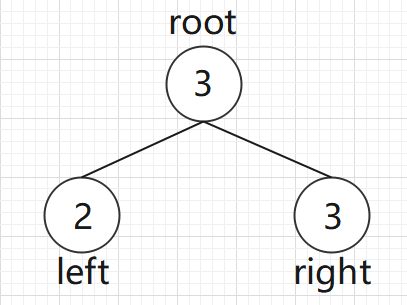
我们以如图所示的二叉树举例：
分类情况
如果不偷根节点，那就要考虑左右孩子要不要偷，即：
root[0] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
如果偷根节点，那么左右孩子都不能偷，即：
root[1] = root.val + left[0] + right[0];
从这里可以看出，无论偷不偷根节点，我们都要对其左右孩子结点操作，也就是说我们需要对二叉树进行后序遍历！
将其推广，则其递推公式为：

//不偷当前结点，左右孩子在偷不偷之间做选择
dp[0] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
//偷当前结点，左右孩子不偷
dp[1] = root.val + left[0] + right[0];

由于是涉及递归，需要对终止条件和单层递归逻辑进行处理，我这里直接贴上代码，思路也比较简单：

class Solution {
    public int rob(TreeNode root) {
        int[] dp = myRob(root);
        return Math.max(dp[0], dp[1]);

    }

    private int[] myRob(TreeNode root) {
        int[] dp = new int[2];
        //终止条件
        if (root == null) {
            return dp;
        }
        //后序遍历先取其左右孩子
        int[] left = myRob(root.left);
        int[] right = myRob(root.right);
        //不偷当前结点，左右孩子在偷不偷之间做选择
        dp[0] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
        //偷当前结点，左右孩子不偷
        dp[1] = root.val + left[0] + right[0];
        return dp;
    }
}

买卖股票

这类题目我只会对二维数组版本进行总结，二维数组思路比较清晰，方便理解与总结，我会在完整代码部分附上空间优化版本。

LeetCode 121. 买卖股票的最佳时机

LeetCode题目链接
动态规划五部曲：

确定dp数组以及下标的含义
本题有两个状态，一个第i天持有股票的价值，另一个记录第i天买入还是卖出，所以需要定义一个二维数组
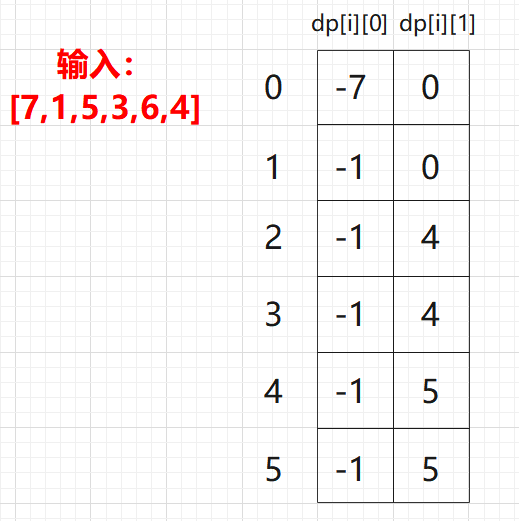
dp[i][0]: 第i天持有股票的最大价值
dp[i][1]: 第i天不持有股票的最大价值
这里的持有很关键，并不是说我第i天一定买入或卖出了股票得到了最大价值，它仅仅表示的是一种状态，我也可能第i - 1天已经卖出了。
确定递推公式
如果第i天持有股票即dp[i][0]，可以由两个状态推导而来

第i - 1天已经持有股票，那就维持原状，即dp[i - 1][0]
第i天买入股票，即-prices[0]
如果第i天不持有股票即dp[i][1]，可以由两个状态推导而来:
第i - 1天也不持有股票，维持原状，即dp[i - 1][1]
第i天卖出股票，那第i - 天就持有股票，将持有股票的价值和第i天卖出的价值相加，即dp[i - 1][0] + prices[i]
综上：
1
2
dp[i][0] = Math.max(dp[i - 1][0], -prices[i]);
dp[i][1] = Math.max(dp[i - 1], dp[i - 1][1] + prices[i]);

dp数组初始化

1 2	dp[0][0] = -prices[0];//第0天持有股票 dp[0][1] = 0;//第0天不持有股票

确定遍历顺序
由状态转移方程可知dp[i]由dp[i - 1]推导而来，所以从前往后遍历。
打印dp数组

完整代码

//二维数组版
class Solution {
    public int maxProfit(int[] prices) {
        if (prices.length < 2) {
            return 0;
        }
        int len = prices.length;
        int[][] dp = new int[len][2];
        dp[0][0] = -prices[0];
        dp[0][1] = 0;
        for (int i = 1; i < len; i++) {
            dp[i][0] = Math.max(dp[i - 1][0], -prices[i]);
            dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] + prices[i]);
        }
        return Math.max(dp[len - 1][0], dp[len - 1][1]);
    }
}

//空间优化版
class Solution {
    public int maxProfit(int[] prices) {
        if (prices.length <= 1) {
            return 0;
        }
        int min = prices[0], max = 0;
        // 第一种情况：最大收益不在最后一天产出，那么就在前i-1天中的某一天
        // 第二种情况：最大收益在组后一天产出，记录前i-1天买入最小值求差值
        for (int i = 1; i < prices.length; i++) {
            max = Math.max(max, prices[i] - min);//max:前i天的最大收益 prices[i] - min：第i天的收益减去前i-1天买入的最小值
            min = Math.min(min, prices[i]);//实时更新买入最小值
        }
        return max;
    }
}

LeetCode 122. 买卖股票的最佳时机 II

LeetCode题目链接
 121. 买卖股票的最佳时机只能购买一支股票，且不能在同一天卖出。
而本题可以买卖多支股票，且可以在同一天卖出，但在任何时候最多只能持有一支股票。
上一题持有股票状态下的递推公式为：dp[i][0] = Math.max(dp[i - 1][0], -prices[i]);
而本题可以购买两次，所以需要对其做一个微小的改动：dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
dp[i - 1][1] - prices[i]：如果在第i天买入，那第i - i天就没有持有。
剩余部分照搬就好：

//二位数组版本
class Solution {
    public int maxProfit(int[] prices) {
        if (prices.length < 2) {
            return 0;
        }
        int len = prices.length;
        int[][] dp = new int[len][2];
        dp[0][0] = -prices[0];
        dp[0][1] = 0;
        for (int i = 1; i < len; i++) {
            dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
            dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] + prices[i]);
        }
        return Math.max(dp[len - 1][0], dp[len - 1][1]);
    }
}

//在评论区看到的脑筋急转弯版本
//扫描一遍 只要后一天比前一天大 就把这两天的差值加一下
class Solution {
    public int maxProfit(int[] prices) {
        int ans = 0;
        for (int i = 1; i <= prices.length - 1; i++) {
            if (prices[i] > prices[i - 1]) {
                ans += prices[i] - prices[i - 1];
            }
        }
        return ans;
    }
}

LeetCode 123. 买卖股票的最佳时机 III

LeetCode题目链接
本题较之前的限制有最多可以完成两笔交易，且必须在再次购买前出售掉之前的股票。
我们之前定义了两种状态来表示买卖一次的状态，那现在可以买卖两次，我们只需要在原来的情况上再叠加一次就好：
dp[i][0] = dp[i - 1][0]: 什么都没做，维持原来状态
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]): 第一次持有
dp[i][2] = Math.max(dp[i - 1][2], dp[i - 1][1] + prices[i]): 第一次卖出
dp[i][3] = Math.max(dp[i - 1][3], dp[i - 1][2] - prices[i]): 第二次持有
dp[i][4] = Math.max(dp[i - 1][4], dp[i - 1][3] + prices[i]): 第二次卖出
同时我们也要初始化四个值:

int[][] dp = new int[len][5];
dp[0][0] = 0;//不操作
dp[0][1] = -prices[0];//第一次持有
dp[0][2] = 0;//第一次卖出
dp[0][3] = -prices[0];//第二次持有
dp[0][4] = 0;//第二次卖出

完整代码：

//二维数组版本
class Solution {
    public int maxProfit(int[] prices) {
        if (prices.length < 2) {
            return 0;
        }
        int len = prices.length;
        int[][] dp = new int[len][5];
        dp[0][0] = 0;//不操作
        dp[0][1] = -prices[0];//第一次持有
        dp[0][2] = 0;//第一次卖出
        dp[0][3] = -prices[0];//第二次持有
        dp[0][4] = 0;//第二次卖出
        for (int i = 1; i < len; i++) {
            dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
            dp[i][2] = Math.max(dp[i - 1][2], dp[i - 1][1] + prices[i]);
            dp[i][3] = Math.max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
            dp[i][4] = Math.max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
        }
        return dp[len - 1][4];
    }
}
//空间优化版本
class Solution {
    public int maxProfit(int[] prices) {
        int[] dp = new int[4];
        // 存储两次交易的状态就行了
        // dp[0]代表第一次交易的买入
        dp[0] = -prices[0];
        // dp[1]代表第一次交易的卖出
        dp[1] = 0;
        // dp[2]代表第二次交易的买入
        dp[2] = -prices[0];
        // dp[3]代表第二次交易的卖出
        dp[3] = 0;
        for (int i = 1; i <= prices.length; i++) {
            // 要么保持不变，要么没有就买，有了就卖
            dp[0] = Math.max(dp[0], -prices[i - 1]);
            dp[1] = Math.max(dp[1], dp[0] + prices[i - 1]);
            // 这已经是第二次交易了，所以得加上前一次交易卖出去的收获
            dp[2] = Math.max(dp[2], dp[1] - prices[i - 1]);
            dp[3] = Math.max(dp[3], dp[2] + prices[i - 1]);
        }
        return dp[3];
    }
}

LeetCode 188. 买卖股票的最佳时机 IV

LeetCode题目链接
与上一题唯一不同的点是股票可以买卖k次
我们知道，一次交易需要记录两种状态(持有/不持有)，那么交易k次就要记录2k种状态，同时我们发现，在初始化时只有dp[i][#] #为基数是才初始为-prices[i]

//二维数组版
class Solution {
    public int maxProfit(int k, int[] prices) {
        if (k == 0 || prices.length < 2) {
            return 0;
        }
        int len = prices.length;
        int[][] dp = new int[len][2 * k + 1];
        for (int i = 1; i < 2 * k; i += 2) {//初始化奇数下标的值
            dp[0][i] = -prices[0];
        }
        for (int i = 1; i < len; i++) {
            for (int j = 0; j < 2 * k; j += 2) {
                dp[i][j + 1] = Math.max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);//持有
                dp[i][j + 2] = Math.max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);//卖出
            }
        }
        return dp[len - 1][2 * k];
    }
}
//空间优化版
class Solution {
    public int maxProfit(int k, int[] prices) {
        if(prices.length == 0){
            return 0;
        }
        if(k == 0){
            return 0;
        }
        // 其实就是123题的扩展，123题只用记录2次交易的状态
        // 这里记录k次交易的状态就行了
        // 每次交易都有买入，卖出两个状态，所以要乘 2
        int[] dp = new int[2 * k];
        // 按123题解题格式那样，做一个初始化
        for(int i = 0; i < dp.length / 2; i++){
            dp[i * 2] = -prices[0];
        }
        for(int i = 1; i <= prices.length; i++){
            dp[0] = Math.max(dp[0], -prices[i - 1]);
            dp[1] = Math.max(dp[1], dp[0] + prices[i - 1]);
            // 还是与123题一样，与123题对照来看
            // 就很容易啦
            for(int j = 2; j < dp.length; j += 2){
                dp[j] = Math.max(dp[j], dp[j - 1] - prices[i-1]);
                dp[j + 1] = Math.max(dp[j + 1], dp[j] + prices[i - 1]);
            }
        }
        // 返回最后一次交易卖出状态的结果就行了
        return dp[dp.length - 1];
    }
}